We consider a rectangular gridworld representation (see below) of a simple finite Markov Decision Process (MDP). The cells of the grid correspond to the states of the environment. At each cell, four actions are possible: north, south, east, and west, which deterministically cause the agent to move one cell in the respective direction on the grid. Actions that would take the agent off the grid leave its location unchanged, but also result in a reward of -1. In other words, rewards are positive for goals, negative for running into undesirable states, and zero the rest of the time.
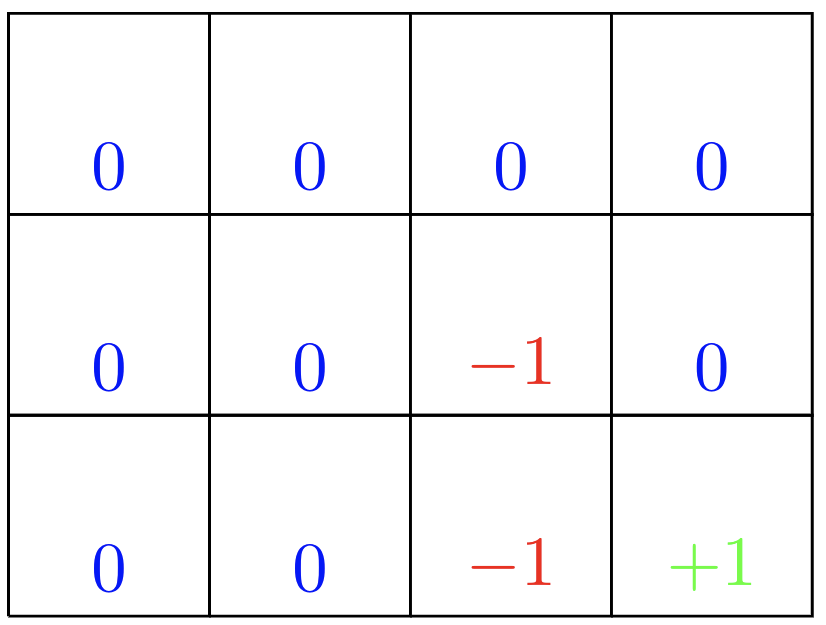
Next we define the rewards for the states. Those will be of +1 for the state that is desirable, of -1 for states that have to be avoided and of 0 for all other states.
The Bellman equation (see below) must hold for each state for the value function \$v_{pi}\$.
\$ v_{pi}(s) = \sum_a \pi(a|s) \sum_{s'|r} p(s',r|s,a) [ r + \gamma v_{\pi}(s') \$ ] , for all \$s \in S\$
where the actions, \$a\$, are taken from the set \$A(s)\$, that the next states, \$s'\$, are taken from the set \$S\$, and that the rewards, \$r\$, are taken from the set \$R\$.
The Bellman equation expresses a relationship between the value of a state and the values of its successor states.
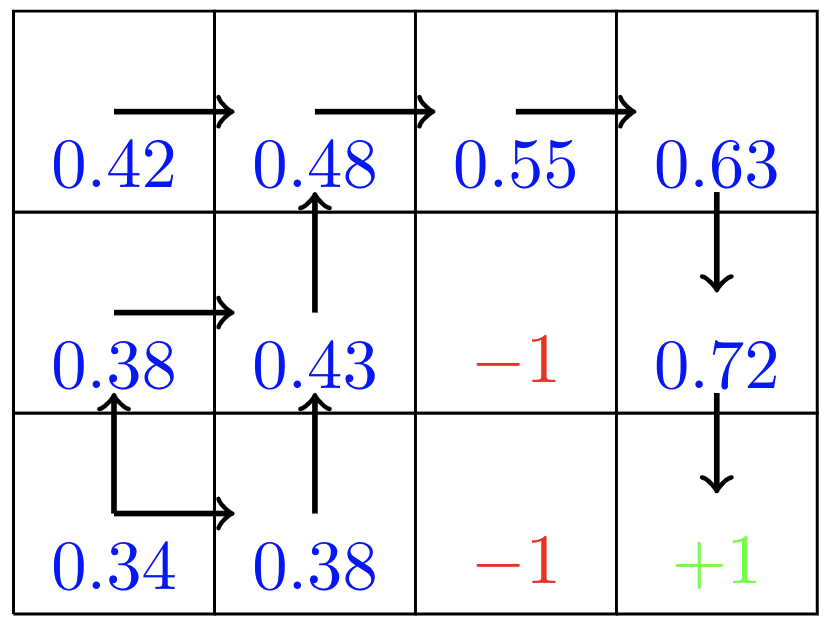
Suppose the agent selects all four actions with equal probability in all states. The figure below shows the value function, \$v_{pi}\$, for this policy, for the discounted reward case with \$\gamma = 0.9\$.
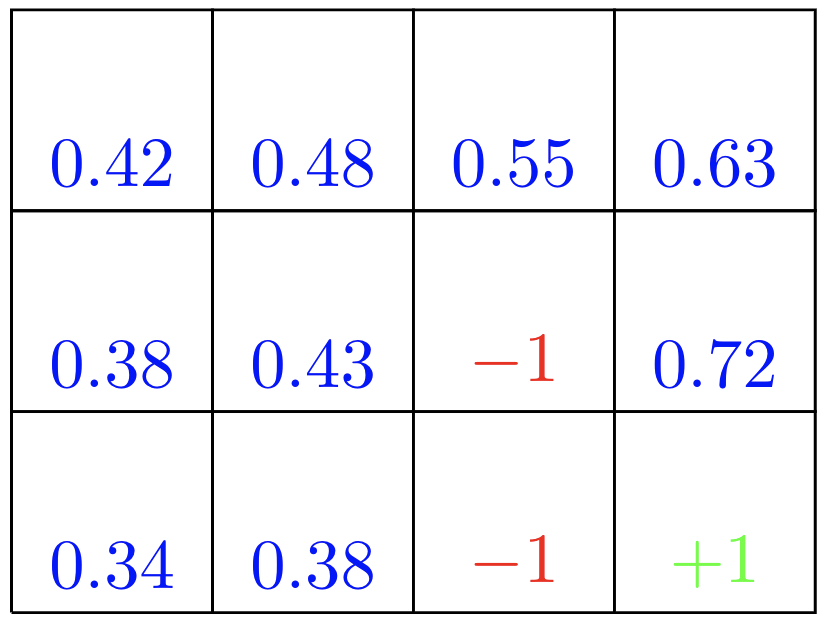
This value function was computed by solving the system of linear equations in the expression for the Bellman equation above.
Source code
import numpy as np
'''==================================================
Initial set up
=================================================='''
#Hyperparameters
SMALL_ENOUGH = 0.005
GAMMA = 0.9
NOISE = 0.1
#Define all states
all_states=[]
for i in range(3):
for j in range(4):
all_states.append((i,j))
#Define rewards for all states
rewards = {}
for i in all_states:
if i == (1,2):
rewards[i] = -1
elif i == (2,2):
rewards[i] = -1
elif i == (2,3):
rewards[i] = 1
else:
rewards[i] = 0
#Dictionnary of possible actions. We have two "end" states (1,2 and 2,2)
actions = {
(0,0):('D', 'R'),
(0,1):('D', 'R', 'L'),
(0,2):('D', 'L', 'R'),
(0,3):('D', 'L'),
(1,0):('D', 'U', 'R'),
(1,1):('D', 'R', 'L', 'U'),
(1,3):('D', 'L', 'U'),
(2,0):('U', 'R'),
(2,1):('U', 'L', 'R'),
}
#Define an initial policy
policy={}
for s in actions.keys():
policy[s] = np.random.choice(actions[s])
#Define initial value function
V={}
for s in all_states:
if s in actions.keys():
V[s] = 0
if s ==(2,2):
V[s]=-1
if s == (1,2):
V[s]=-1
if s == (2,3):
V[s]=1
'''==================================================
Value Iteration
=================================================='''
iteration = 0
while True:
biggest_change = 0
for s in all_states:
if s in policy:
old_v = V[s]
new_v = 0
for a in actions[s]:
if a == 'U':
nxt = [s[0]-1, s[1]]
if a == 'D':
nxt = [s[0]+1, s[1]]
if a == 'L':
nxt = [s[0], s[1]-1]
if a == 'R':
nxt = [s[0], s[1]+1]
#Choose a new random action to do (transition probability)
random_1=np.random.choice([i for i in actions[s] if i != a])
if random_1 == 'U':
act = [s[0]-1, s[1]]
if random_1 == 'D':
act = [s[0]+1, s[1]]
if random_1 == 'L':
act = [s[0], s[1]-1]
if random_1 == 'R':
act = [s[0], s[1]+1]
#Calculate the value
nxt = tuple(nxt)
act = tuple(act)
v = rewards[s] + (GAMMA * ((1-NOISE)* V[nxt] + (NOISE * V[act])))
if v > new_v: #Is this the best action so far? If so, keep it
new_v = v
policy[s] = a
#Save the best of all actions for the state
V[s] = new_v
biggest_change = max(biggest_change, np.abs(old_v - V[s]))
#See if the loop should stop now
if biggest_change < SMALL_ENOUGH:
break
iteration += 1Sources:
-
Sutton and Barto. Reinforcement Learning
-
How To Code The Value Iteration Algorithm For Reinforcement Learning